
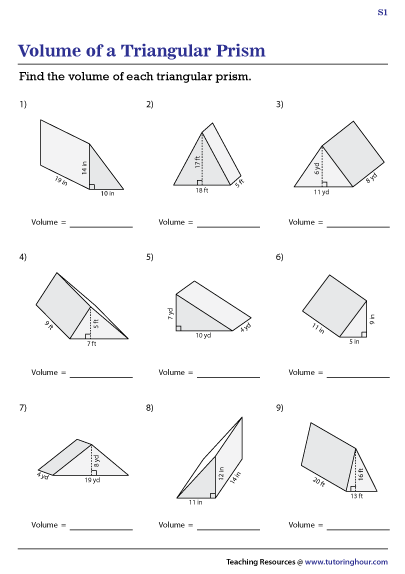
You need just two measurements: the diameter of the base and it's height, but the calculus is more involved than most of the other simple bodies. The surface area of a cone is one of the most complicated and it is where the need for a calculator becomes more apparent. The surface area formula for a cone, given its diameter (or radius) and height is π x (diameter / 2) 2 + π x (diameter / 2) x √ ((diameter / 2) 2 + (height 2)), where (diameter / 2) is the radius of the base (d = 2 x r), so another way to write it is π x radius 2 + π x radius x √ (radius 2 + (height 2)), as seen in the figure below: To find the SA simply multiply 4 times 3.14159 times the radius square. The area of the triangle at the front is 1 2 ×12×530cm2 21 × 12 × 5 30cm2 The back face is the same as the front face so the area of the back is also 30cm2 30cm2. π is, of course, the well-known mathematical constant, about equal to 3.14159. Work out the surface area of the triangular prism Work out the area of each face. Visual on the figure below:Ī sphere's surface area can be calculated just by knowing its diameter, or radius (diameter = 2 x radius). The surface area formula for a sphere is 4 x π x (diameter / 2) 2, where (diameter / 2) is the radius of the sphere (d = 2 x r), so another way to write it is 4 x π x radius 2. side 2 is the surface of one of the sides, and since the cube has 6 equal sides, multiplying by 6 gives us the total cube surface area. This calculation requires only one measurement, due to the symmetricity of the cube. The surface area formula for a cube is 6 x side 2, as seen in the figure below: In this lesson, students will calculate the surface area of triangular prisms. The result from our surface area calculator will always be a square of the same unit: square feet, square inches, square meters, square cm, square mm. Solution: From the image, we can observe that the side lengths of the triangle are a 5 cm, b 6 cm and c 5 cm. In all surface area calculations, make sure that all lengths are measured in the same unit, e.g. Example 1: Find the surface area of the triangular prism with the measurements seen in the image. Finding the surface area of nets will be fun with this colorful and easy to use geometry activityOpen the product preview to see examples of the types of problems included.
Below are the formulas for calculating surface area of the most common body types. Students will practice finding the surface area of pyramids and the surface area of prisms with this set of task cards.
Find the surface area and volume of triangular prism how to#
How to calculate the surface area of a body?ĭepending on the type of body, there are different formulas and different required information you need to calculate surface area (a.k.a.


 0 kommentar(er)
0 kommentar(er)
